OR less click-baity: What is the maximum Bayes factor you can get for a given p value? (Obvious disclaimer: Don’t cheat)
Starting to use and interpret Bayesian statistics can be hard at first. A recent recommendation that I like is from Zoltan Dienes and Neil Mclatchie, to “Report a B for every p.” Meaning, for every p value in the paper report a corresponding Bayes factor. This way the psychology community can start to build an intuition about how these two kinds of results can correspond. I think this is a great way to start using Bayes. And if as time goes on you want to flush those ps down the toilet, I won’t complain.
Researchers who start to report both Bayesian and frequentist results often go through a phase where they are surprised to find that their p<.05 results correspond to weak Bayes factors. In this Understanding Bayes post I hope to pump your intuitions a bit as to why this is the case. There is, in fact, an absolute maximum Bayes factor for a given p value. There are also other soft maximums it can achieve for different classes of prior distributions. And these maximum BFs may not be as high as you expect.
Absolute Maximum
The reason for the absolute maximum is actually straightforward. The Bayes factor compares how accurately two or more competing hypotheses predict the observed data. Usually one of those hypotheses is a point null hypothesis, which says there is no effect in the population (however defined). The alternative can be anything you like. It could be a point hypothesis motivated by theory or that you take from previous literature (uncommon), or it can be a (half-)normal (or other) distribution centered on the null (more common), or anything else. In any case, the fact is that to achieve the absolute maximum Bayes factor for a given p value you have to cheat. In real life you can never reach the absolute maximum in a normal course of analysis so its only use is as a benchmark illustration.
You have to make your alternative hypothesis the exact point hypothesis that maximizes the likelihood of the data. The likelihood function ranks all the parameter values by how well they predict the data, so if you make your point hypothesis equal to the mode of the likelihood function, it means that no other hypothesis or population parameter could make the data more likely. This illicit prior is known as the oracle prior, because it is the prior you would choose if you could see the result ahead of time. So in the figure below, the oracle prior would correspond to the high dot on the curve at the mode, and the null hypothesis is the lower dot on the curve. The Bayes factor is then just the ratio of these heights.
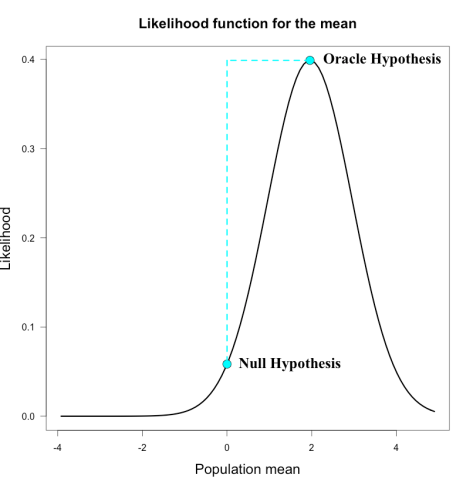
When you are doing a t-test, for example, the maximum of the likelihood function is simply the sample mean. So in this case, the oracle prior is a point hypothesis at exactly the sample mean. Let’s assume that we know the population SD=10, so we’re only interested in the population mean. We collect 100 participants and the sample mean we get is 1.96. Our z score in this case is
z = mean / standard error = 1.96 / (10/√100) = 1.96.
This means we obtain a p value of exactly .05. Publication and glory await us. But, in sticking with our B for every p mantra, we decide to calculate an oracle Bayes factor just to be complete. This can easily be done in R using the following 1 line of code:
dnorm(1.96, 1.96, 1)/dnorm(1.96, 0, 1)
And the answer you get is BF = 6.83. This is the absolute maximum Bayes factor you can possibly get for a p value that equals .05 in a t test (you get similar BFs for other types of tests). That is the amount of evidence that would bring a neutral reader who has prior probabilities of 50% for the null and 50% for the alternative to posterior probabilities of 12.8% for the null and 87.2% for the alternative. You might call that moderate evidence depending on the situation. For p of .01, this maximum increases to ~27.5, which is quite strong in most cases. But these values are for the best case ever, where you straight up cheat. When you can’t blatantly cheat the results are not so good.
Soft Maximum
Of course, nobody in their right mind would accept your analysis if you used an oracle prior. It is blatant cheating — but it gives a good benchmark. For p of .05 and the oracle prior, the best BF you can ever get is slightly less than 7. If you can’t blatantly cheat by using an oracle prior, the maximum Bayes factor you can get obviously won’t be as high. But it may surprise you how much smaller the maximum becomes if you decide to cheat more subtly.
The priors most people use for the alternative hypothesis in the Bayes factor are not point hypotheses, but distributed hypotheses. A common recommendation is a unimodal (i.e., one-hump) symmetric prior centered on the null hypothesis value. (There are times where you wouldn’t want to use a prior centered on the null value, but in those cases the maximum BF goes back to being the BF you get using an oracle prior.) I usually recommend using normal distribution priors, and JASP software uses a Cauchy distribution which is similar but with fatter tails. Most of the time the BFs you get are very similar.
So imagine that instead of using the blatantly cheating oracle prior, you use a subtle oracle prior. Instead of a point alternative at the observed mean, you use a normal distribution and pick the scale (i.e., the SD) of your prior to maximize the Bayes factor. There is a formula for this, but the derivation is very technical so I’ll let you read Berger and Sellke (1987, especially section 3) if you’re into that sort of torture.
It turns out, once you do the math, that when using a normal distribution prior the maximum Bayes factor you can get for a p value of .05 is BF = 2.1. That is the amount of evidence that would bring a neutral reader who has prior probabilities of 50% for the null and 50% for the alternative to posterior probabilities of 32% for the null and 68% for the alternative. Barely different! That is very weak evidence. The maximum normal prior BF corresponding to p of .01 is BF = 6.5. That is still hardly convincing evidence! You can find this bound for any t value you like (for any t greater than 1) using the R code below:
t = 1.96
maxBF = 1/(sqrt(exp(1))*t*exp(-t^2/2))
(You can get slightly different maximum values for different formulations of problem. Another form due to Sellke, Bayarri, & Berger [2001] is 1/[-e*p*ln(p)] for p<~.4, which for p=.05 returns BF = 2.45)
You might say, “Wait no I have a directional prediction, so I will use a half-normal prior that allows only positive values for the population mean. What is my maximum BF now?” Luckily the answer is simple: Just multiply the old maximum by:
2*(1 – p/2)
So for p of .05 and .01 the maximum 1-sided BFs are 4.1 and 13, respectively. (By the way, this trick works for converting most common BFs from 2- to 1-sided.)
Take home message
Do not be surprised if you start reporting Bayes factors and find that what you thought was strong evidence based on a p value of .05 or even .01 translates to a quite weak Bayes factor.
And I think this goes without saying, but don’t try to game your Bayes factors. We’ll know. It’s obvious. The best thing to do is use the prior distribution you find most reasonable for the problem at hand and then do a robustness check by seeing how much the conclusion you draw depends on the specific prior you choose. JASP software can do this for you automatically in many cases (e.g., for the Bayesian t-test; ps check out our official JASP tutorial videos!).
R code
The following is the R code to reproduce the figure, to find the max BF for oracle priors, and to find the max BF for subtle oracle priors. Tinker with it and see how your intuitions match the answers you get!
| #This is the code for Alexander Etz's blog at http://wp.me/p4sgtg-SQ | |
| #Code to make the figure and find max oracle BF for normal data | |
| maxL <- function(mean=1.96,se=1,h0=0){ | |
| L1 <-dnorm(mean,mean,se) | |
| L2 <-dnorm(mean,h0,se) | |
| Ratio <- L1/L2 | |
| curve(dnorm(x,mean,se), xlim = c(-2*mean,2.5*mean), ylab = "Likelihood", xlab = "Population mean", las=1, | |
| main = "Likelihood function for the mean", lwd = 3) | |
| points(mean, L1, cex = 2, pch = 21, bg = "cyan") | |
| points(h0, L2, cex = 2, pch = 21, bg = "cyan") | |
| lines(c(mean, h0), c(L1, L1), lwd = 3, lty = 2, col = "cyan") | |
| lines(c(h0, h0), c(L1, L2), lwd = 3, lty = 2, col = "cyan") | |
| return(Ratio) ## Returns the Bayes factor for oracle hypothesis vs null | |
| } | |
| #Code to find the max subtle oracle prior BF for normal data | |
| t = 1.96 #Critical value corresponding to the p value | |
| maxBF = 1/(sqrt(exp(1))*t*exp(-t^2/2)) #Formula from Berger and Sellke 1987 | |
| #multiply by 2*(1-p/2) if using a one-sided prior | |
It occurs to me that what you refer to here as a Bayes factor w/ oracle prior is better known as… a likelihood ratio! Which I find pretty interesting, because this gives an alternative and somewhat less flattering perspective on the logic behind the likelihood ratio test — a test that of course is used extremely frequently, even though from this perspective it is “blatant cheating.”