probability

A quick comment on recent BF (vs p-value) error control blog posts

Alex Etz Statistics , , , , , ,

There have recently been two stimulating posts regarding error control for Bayes factors. (Stimulating enough to get me to write this, at least.) Daniel Lakens commented on how Bayes factors can vary across studies due to sampling error. Tim van der Zee compared the type 1 and type 2 error rates for using p-values versus using BFs. My comment is not so much to pass judgment on the content of the posts (other than this quick note that they are not really proper Bayesian simulations), but to suggest an easier way to do what they are already doing. They both use simulations to get their error rates (which can take ages when you have lots of groups), but in this post I’d like to show a way to find the exact same answers without simulation, by just thinking about the problem from a slightly different angle.

Lakens and van der Zee both set up their simulations as follows: For a two sample t-test, assume a true underlying population effect size (i.e., δ), a fixed sample size per group (n1 and n2),  and calculate a Bayes factor comparing a point null versus an alternative hypothesis that assigns δ a prior distribution of Cauchy(0, .707) [the default prior for the Bayesian t-test]. Then simulate a bunch of sample t-values from the underlying effect size, plug them into the BayesFactor R package, and see what proportion of BFs are above, below or between certain values (both happen to focus on 3 and 1/3). [This is a very common simulation setup that I see in many blogs these days.]

I’ll just use a couple of representative examples from van der Zee’s post to show how to do this. Let’s say n1 = n2 = 50 and we use the default Cauchy prior on the alternative. In this setup, one can very easily calculate the resulting BF for any observed t-value using the BayesFactor R package. A BF of 3 corresponds to an observed | t | = ~2.47; a BF of 1/3 corresponds to | t | = ~1. These are your critical t values. Any t value greater than 2.47 (or less than -2.47) will have a BF > 3. Any t value between -1 and 1 will have BF < 1/3. Any t value between 1 and 2.47 (or between -1 and -2.47) will have 1/3 < BF < 3. All we have to do now is find out what proportion of sample t values would fall in these regions for the chosen underlying effect size, which is done by finding the area of the sampling distribution between the various critical values.

easier type 1 errors

If the underlying effect size for the simulation is δ = 0 (i.e., the null hypothesis is true), then observed t-values will follow the typical central t-distribution. For 98 degrees of freedom, this looks like the following.

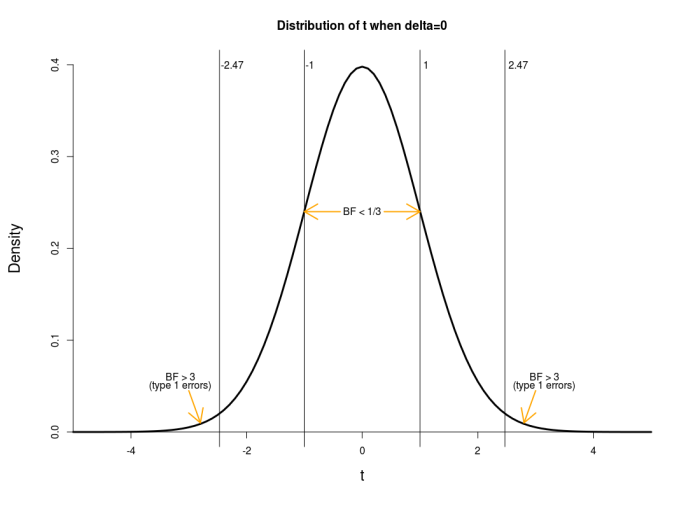
Rplot05

I have marked the critical t values for BF = 3 and BF = 1/3 found above. van der Zee denotes BF > 3 as type 1 errors when δ = 0. The type 1 error rate is found by calculating the area under this curve in the tails beyond | t | = 2.47. A simple line in r gives the answer:

2*pt(-2.47,df=98)
[.0152]

The type 1 error rate is thus 1.52% (van der Zee’s simulations found 1.49%, see his third table). van der Zee notes that this is much lower than the type 1 error rate of 5% for the frequentist t test (the area in the tails beyond | t | = 1.98) because the t criterion is much higher for a Bayes factor of 3 than a p value of .05.  [As an aside, if one wanted the BF criterion corresponding to a type 1 error rate of 5%, it is BF > 1.18 in this case (i.e., this is the BF obtained from | t | = 1.98). That is, for this setup, 5% type 1 error rate is achieved nearly automatically.]

The rate at which t values fall between -2.47 and -1 and between 1 and 2.47 (i.e., find 1/3 < BF < 3) is the area of this curve between -2.47 and -1 plus the area between 1 and 2.47, found by:

2*(pt(-1,df=98)-pt(-2.47,df=98))
[1] 0.3045337

The rate at which t values fall between -1 and 1 (i.e., find BF < 1/3) is the area between -1 and 1, found by:

pt(1,df=98)-pt(-1,df=98)
[1] 0.6802267

easier type 2 errors

If the underlying effect size for the simulation is changed to δ  = .4 (another one of van der Zee’s examples, and now similar to Lakens’s example), the null hypothesis is then false and the relevant t distribution is no longer centered on zero (and is asymmetric). To find the new sampling distribution, called the noncentral t-distribution, we need to find the noncentrality parameter for the t-distribution that corresponds to δ = .4 when n1 = n2 = 50. For a two-sample t test, this is found by a simple formula, ncp = δ / √(1/n1 + 1/n2); in this case we have ncp = .4 / √(1/50 + 1/50) = 2. The noncentral t-distribution for δ=.4 and 98 degrees of freedom looks like the following.

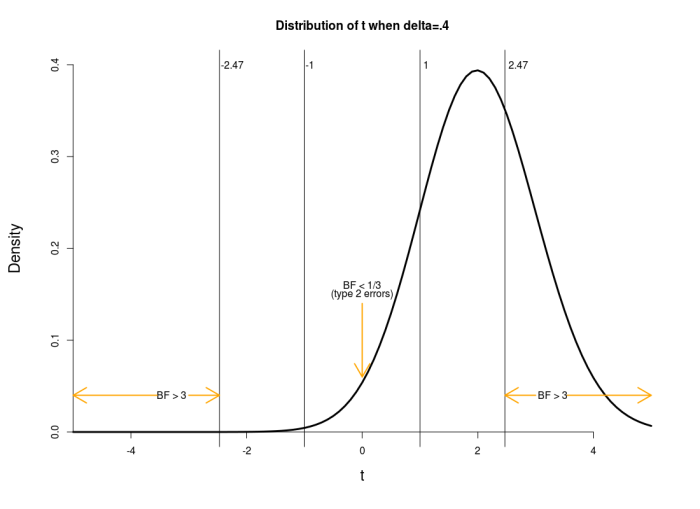
deltazero

I have again marked the relevant critical values. van der Zee denotes BF < 1/3 as type 2 errors when δ ≠ 0 (and Lakens is also interested in this area). The rate at which this occurs is once again the area under the curve between -1 and 1, found by:

pt(1,df=98,ncp=2)-pt(-1,df=98,ncp=2)
[1] 0.1572583

The type 2 error rate is thus 15.7% (van der Zee’s simulation finds 16.8%, see his first table). The other rates of interest are similarly found.

Conclusion

You don’t necessarily need to simulate this stuff! You can save a lot of simulation time by working it out with a little arithmetic plus a few easy lines of code.

 

 

Understanding Bayes: How to cheat to get the maximum Bayes factor for a given p value

Alex Etz Psychology, Statistics, Understanding Bayes , , , , , , ,

OR less click-baity: What is the maximum Bayes factor you can get for a given p value? (Obvious disclaimer: Don’t cheat)

Starting to use and interpret Bayesian statistics can be hard at first. A recent recommendation that I like is from Zoltan Dienes and Neil Mclatchie, to “Report a B for every p.” Meaning, for every p value in the paper report a corresponding Bayes factor. This way the psychology community can start to build an intuition about how these two kinds of results can correspond. I think this is a great way to start using Bayes. And if as time goes on you want to flush those ps down the toilet, I won’t complain.

Researchers who start to report both Bayesian and frequentist results often go through a phase where they are surprised to find that their p<.05 results correspond to weak Bayes factors. In this Understanding Bayes post I hope to pump your intuitions a bit as to why this is the case. There is, in fact, an absolute maximum Bayes factor for a given p value. There are also other soft maximums it can achieve for different classes of prior distributions. And these maximum BFs may not be as high as you expect.

Absolute Maximum

The reason for the absolute maximum is actually straightforward. The Bayes factor compares how accurately two or more competing hypotheses predict the observed data. Usually one of those hypotheses is a point null hypothesis, which says there is no effect in the population (however defined). The alternative can be anything you like. It could be a point hypothesis motivated by theory or that you take from previous literature (uncommon), or it can be a (half-)normal (or other) distribution centered on the null (more common), or anything else. In any case, the fact is that to achieve the absolute maximum Bayes factor for a given p value you have to cheat. In real life you can never reach the absolute maximum in a normal course of analysis so its only use is as a benchmark illustration.

You have to make your alternative hypothesis the exact point hypothesis that maximizes the likelihood of the data. The likelihood function ranks all the parameter values by how well they predict the data, so if you make your point hypothesis equal to the mode of the likelihood function, it means that no other hypothesis or population parameter could make the data more likely. This illicit prior is known as the oracle prior, because it is the prior you would choose if you could see the result ahead of time. So in the figure below, the oracle prior would correspond to the high dot on the curve at the mode, and the null hypothesis is the lower dot on the curve. The Bayes factor is then just the ratio of these heights.

When you are doing a t-test, for example, the maximum of the likelihood function is simply the sample mean. So in this case, the oracle prior is a point hypothesis at exactly the sample mean. Let’s assume that we know the population SD=10, so we’re only interested in the population mean. We collect 100 participants and the sample mean we get is 1.96. Our z score in this case is

z = mean / standard error = 1.96 / (10/√100) = 1.96.

This means we obtain a p value of exactly .05. Publication and glory await us. But, in sticking with our B for every p mantra, we decide to calculate an oracle Bayes factor just to be complete. This can easily be done in R using the following 1 line of code:

dnorm(1.96, 1.96, 1)/dnorm(1.96, 0, 1)

And the answer you get is BF = 6.83. This is the absolute maximum Bayes factor you can possibly get for a p value that equals .05 in a t test (you get similar BFs for other types of tests). That is the amount of evidence that would bring a neutral reader who has prior probabilities of 50% for the null and 50% for the alternative to posterior probabilities of 12.8% for the null and 87.2% for the alternative. You might call that moderate evidence depending on the situation. For p of .01, this maximum increases to ~27.5, which is quite strong in most cases. But these values are for the best case ever, where you straight up cheat. When you can’t blatantly cheat the results are not so good.

Soft Maximum

Of course, nobody in their right mind would accept your analysis if you used an oracle prior. It is blatant cheating — but it gives a good benchmark. For p of .05 and the oracle prior, the best BF you can ever get is slightly less than 7. If you can’t blatantly cheat by using an oracle prior, the maximum Bayes factor you can get obviously won’t be as high. But it may surprise you how much smaller the maximum becomes if you decide to cheat more subtly.

The priors most people use for the alternative hypothesis in the Bayes factor are not point hypotheses, but distributed hypotheses. A common recommendation is a unimodal (i.e., one-hump) symmetric prior centered on the null hypothesis value. (There are times where you wouldn’t want to use a prior centered on the null value, but in those cases the maximum BF goes back to being the BF you get using an oracle prior.) I usually recommend using normal distribution priors, and JASP software uses a Cauchy distribution which is similar but with fatter tails. Most of the time the BFs you get are very similar.

So imagine that instead of using the blatantly cheating oracle prior, you use a subtle oracle prior. Instead of a point alternative at the observed mean, you use a normal distribution and pick the scale (i.e., the SD) of your prior to maximize the Bayes factor. There is a formula for this, but the derivation is very technical so I’ll let you read Berger and Sellke (1987, especially section 3) if you’re into that sort of torture.

It turns out, once you do the math, that when using a normal distribution prior the maximum Bayes factor you can get for a p value of .05 is BF = 2.1. That is the amount of evidence that would bring a neutral reader who has prior probabilities of 50% for the null and 50% for the alternative to posterior probabilities of 32% for the null and 68% for the alternative. Barely different! That is very weak evidence. The maximum normal prior BF corresponding to p of .01 is BF = 6.5. That is still hardly convincing evidence! You can find this bound for any t value you like (for any t greater than 1) using the R code below:

t = 1.96
maxBF = 1/(sqrt(exp(1))*t*exp(-t^2/2))

(You can get slightly different maximum values for different formulations of problem. Another form due to Sellke, Bayarri, & Berger [2001] is 1/[-e*p*ln(p)] for p<~.4, which for p=.05 returns BF = 2.45)

You might say, “Wait no I have a directional prediction, so I will use a half-normal prior that allows only positive values for the population mean. What is my maximum BF now?” Luckily the answer is simple: Just multiply the old maximum by:

2*(1 – p/2)

So for p of .05 and .01 the maximum 1-sided BFs are 4.1 and 13, respectively. (By the way, this trick works for converting most common BFs from 2- to 1-sided.)

Take home message

Do not be surprised if you start reporting Bayes factors and find that what you thought was strong evidence based on a p value of .05 or even .01 translates to a quite weak Bayes factor.

And I think this goes without saying, but don’t try to game your Bayes factors. We’ll know. It’s obvious. The best thing to do is use the prior distribution you find most reasonable for the problem at hand and then do a robustness check by seeing how much the conclusion you draw depends on the specific prior you choose. JASP software can do this for you automatically in many cases (e.g., for the Bayesian t-test; ps check out our official JASP tutorial videos!).

R code

The following is the R code to reproduce the figure, to find the max BF for oracle priors, and to find the max BF for subtle oracle priors. Tinker with it and see how your intuitions match the answers you get!

#This is the code for Alexander Etz's blog at http://wp.me/p4sgtg-SQ
#Code to make the figure and find max oracle BF for normal data
maxL <- function(mean=1.96,se=1,h0=0){
L1 <-dnorm(mean,mean,se)
L2 <-dnorm(mean,h0,se)
Ratio <- L1/L2
curve(dnorm(x,mean,se), xlim = c(-2*mean,2.5*mean), ylab = "Likelihood", xlab = "Population mean", las=1,
main = "Likelihood function for the mean", lwd = 3)
points(mean, L1, cex = 2, pch = 21, bg = "cyan")
points(h0, L2, cex = 2, pch = 21, bg = "cyan")
lines(c(mean, h0), c(L1, L1), lwd = 3, lty = 2, col = "cyan")
lines(c(h0, h0), c(L1, L2), lwd = 3, lty = 2, col = "cyan")
return(Ratio) ## Returns the Bayes factor for oracle hypothesis vs null
}
#Code to find the max subtle oracle prior BF for normal data
t = 1.96 #Critical value corresponding to the p value
maxBF = 1/(sqrt(exp(1))*t*exp(-t^2/2)) #Formula from Berger and Sellke 1987
#multiply by 2*(1-p/2) if using a one-sided prior
view raw MaxBF.R hosted with ❤ by GitHub

 

 

Sunday Bayes: A brief history of Bayesian stats

Alex Etz Article Review, Statistics , , ,

The following discussion is essentially nontechnical; the aim is only to convey a little introductory “feel” for our outlook, purpose, and terminology, and to alert newcomers to common pitfalls of understanding.

Sometimes, in our perplexity, it has seemed to us that there are two basically different kinds of mentality in statistics; those who see the point of Bayesian inference at once, and need no explanation; and those who never see it, however much explanation is given.

–Jaynes, 1986 (pdf link)

Sunday Bayes

The format of this series is short and simple: Every week I will give a quick summary of a paper while sharing a few excerpts that I like. If you’ve read our eight easy steps paper and you’d like to follow along on this extension, I think a pace of one paper per week is a perfect way to ease yourself into the Bayesian sphere.

Bayesian Methods: General Background

The necessity of reasoning as best we can in situations where our information is incomplete is faced by all of us, every waking hour of our lives. (p. 2)

In order to understand Bayesian methods, I think it is essential to have some basic knowledge of their history. This paper by Jaynes (pdf) is an excellent place to start.

[Herodotus] notes that a decision was wise, even though it led to disastrous consequences, if the evidence at hand indicated it as the best one to make; and that a decision was foolish, even though it led to the happiest possible consequences, if it was unreasonable to expect those consequences. (p. 2)

Jaynes traces the history of Bayesian reasoning all the way back to Herodotus in 500BC. Herodotus could hardly be called a Bayesian, but the above quote captures the essence of Bayesian decision theory: take the action that maximizes your expected gain. It may turn out to be the wrong choice in the end, but if your reasoning that leads to your choice is sound then you took the correct course.

After all, our goal is not omniscience, but only to reason as best we can with whatever incomplete information we have. To demand more than this is to demand the impossible; neither Bernoulli’s procedure nor any other that might be put in its place can get something for nothing. (p. 3)

Much of the foundation for Bayesian inference was actually laid down by James Bernoulli, in his work Ars Conjectandi (“the art of conjecture”) in 1713. Bernoulli was the first to really invent a rational way of specifying a state of incomplete information. He put forth the idea that one can enumerate all “equally possible” cases N, and then count the number of cases for which some event A can occur. Then the probability of A, call it p(A), is just M/N, or the number of cases on which A can occur (M) to the total number of cases (N).

Jaynes gives only a passing mention to Bayes, noting his work “had little if any direct influence on the later development of probability theory” (p. 5). Laplace, Jeffreys, Cox, and Shannon all get a thorough discussion, and there is a lot of interesting material in those sections.

Despite the name, Bayes’ theorem was really formulated by Laplace. By all accounts, we should all be Laplacians right now.

The basic theorem appears today as almost trivially simple; yet it is by far the most important principle underlying scientific inference. (p. 5)

Laplace used Bayes’ theorem to estimate the mass of Saturn, and, by the best estimates when Jaynes was writing, his estimate was correct within .63%. That is very impressive for work done in the 18th century!

This strange history is only one of the reasons why, today [speaking in 1984], we Bayesians need to take the greatest pains to explain our rationale, as I am trying to do here. It is not that it is technically complicated; it is the way we have all been thinking intuitively from childhood. It is just so different from what we were all taught in formal courses on “orthodox” probability theory, which paralyze the mind into an inability to see a distinction between probability and frequency. Students who come to us free of that impediment have no difficulty in understanding our rationale, and are incredulous to anyone that could fail to understand it. (p. 7)

The sections on Laplace, Jeffreys, Cox and Shannon are all very good, but I will skip most of them because I think the most interesting and illuminating section of this paper is “Communication Difficulties” beginning on page 10.

Our background remarks would be incomplete without taking note of a serious disease that has afflicted probability theory for 200 years. There is a long history of confusion and controversy, leading in some cases to a paralytic inability to communicate. (p.10)

Jaynes is concerned in this section with the communication difficulties that Bayesians and frequentists have historically encountered.

[Since the 1930s] there has been a puzzling communication block that has prevented orthodoxians [frequentists] from comprehending Bayesian methods, and Bayesians from comprehending orthodox criticisms of our methods. (p. 10)

On the topic of this disagreement, Jaynes gives a nice quote from L.J. Savage: “there has seldom been such complete disagreement and breakdown of communication since the tower of Babel.” I wrote about one kind of communication breakdown in last week’s Sunday Bayes entry.

So what is the disagreement that Jaynes believes underlies much of the conflict between Bayesians and frequentists?

For decades Bayesians have been accused of “supposing that an unknown parameter is a random variable”; and we have denied hundreds of times with increasing vehemence, that we are making any such assumption. (p. 11)

Jaynes believes the confusion can be made clear by rephrasing the criticism as George Barnard once did.

Barnard complained that Bayesian methods of parameter estimation, which present our conclusions in the form of a posterior distribution, are illogical; for “How could the distribution of a parameter possibly become known from data which were taken with only one value of the parameter actually present?” (p. 11)

Aha, this is a key reformulation! This really illuminates the confusions between frequentists and Bayesians. To show why I’ll give one long quote to finish this Sunday Bayes entry.

Orthodoxians trying to understand Bayesian methods have been caught in a semantic trap by their habitual use of the phrase “distribution of the parameter” when one should have said “distribution of the probability”. Bayesians had supposed this to be merely a figure of speech; i.e., that those who used it did so only out of force of habit, and really knew better. But now it seems that our critics  have been taking that phraseology quite literally all the time.

Therefore, let us belabor still another time what we had previously thought too obvious to mention. In Bayesian parameter estimation, both the prior and posterior distributions represent, not any measurable property of the parameter, but only our own state of knowledge about it. The width of the distribution is not intended to indicate the range of variability of the true values of the parameter, as Barnards terminology had led him to suppose. It indicates the range of values that are consistent with our prior information and data, and which honesty therefore compels us to admit as possible values. What is “distributed” is not the parameter, but the probability. [emphasis added]

Now it appears that, for all these years, those who have seemed immune to all Bayesian explanation have just misunderstood our purpose. All this time, we had thought it clear from our subject-matter context that we are trying to estimate the value that the parameter had at the time the data were taken. [emphasis original] Put more generally, we are trying to draw inferences about what actually did happen in the experiment; not about the things that might have happened but did not. (p. 11)

I think if you really read the section on communication difficulties closely, then you will see that a lot of the conflict between Bayesians and frequentists can be boiled down to deep semantic confusion. We are often just talking past one another, getting ever more frustrated that the other side doesn’t understand our very simple points. Once this is sorted out I think a lot of the problems frequentists see with Bayesian methods will go away.

Video: “A Bayesian Perspective of the Reproducibility Project: Psychology”

Alex Etz Psychology, Statistics , , , , , , ,

I recently gave a talk at the University of Bristol’s Medical Research Council Integrative Epidemiology Unit, titled, “A Bayesian Perspective on the Reproducibility Project: Psychology,” in which I recount the results from our recently published Bayesian reanalysis of the RPP (you can read it in PLOS ONE). In that paper Joachim Vandekerckhove and I reassessed the evidence from the RPP and found that most of the original and replication studies only managed to obtain weak evidence.

I’m very grateful to Marcus Munafo for inviting me out to give this talk. And I’m also grateful to Jim Lumsden for help organizing. We recorded the talk’s audio and synced it to a screencast of my slides, so if you weren’t there you can still hear about it. 🙂

I’ve posted the slides on slideshare, and you can download a copy of the presentation by clicking here. (It says 83 slides, but the last ~30 slides are a technical appendix prepared for the Q&A)

If you think this is interesting and you’d like to learn more about Bayes, you can check out my Understanding Bayes tutorial series and also our paper, “How to become a Bayesian in eight easy steps.”

Sunday Bayes: Optional stopping is no problem for Bayesians

Alex Etz Article Review, Statistics , , , , ,

Optional stopping does not affect the interpretation of posterior odds. Even with optional stopping, a researcher can interpret the posterior odds as updated beliefs about hypotheses in light of data.

–Rouder, 2014 (pdf link)

Sunday Bayes

The format of this series is short and simple: Every week I will give a quick summary of a paper while sharing a few excerpts that I like. If you’ve read our eight easy steps paper and you’d like to follow along on this extension, I think a pace of one paper per week is a perfect way to ease yourself into the Bayesian sphere.

Optional stopping: No problem for Bayesians

Bayesian analysts use probability to express a degree of belief. For a flipped coin, a probability of 3/4 means that the analyst believes it is three times more likely that the coin will land heads than tails. Such a conceptualization is very convenient in science, where researchers hold beliefs about the plausibility of theories, hypotheses, and models that may be updated as new data become available. (p. 302)

It is becoming increasingly common to evaluate statistical procedures by way of simulation. Instead of doing formal analyses, we can use flexible simulations to tune many different parameters and immediately see the effect it has on the behavior of a procedure.

Simulation results have a tangible, experimental feel; moreover, if something is true mathematically, we should be able to see it in simulation as well. (p. 303)

But this brings with it a danger that the simulations performed might be doing the wrong thing, and unless we have a good grasp of the theoretical background of what is being simulated we can easily be misled. In this paper, Rouder (pdf) shows that common intuitions we have for evaluating simulations of frequentist statistics often do not translate to simulations of Bayesian statistics.

The critical element addressed here is whether optional stopping is problematic for Bayesians. My  argument is that both sets of authors use the wrong criteria or lens to draw their conclusions. They evaluate and interpret Bayesian statistics as if they were frequentist statistics. The more germane question is whether Bayesian statistics are interpretable as Bayesian statistics even if data are collected under optional stopping. (p. 302)

When we evaluate a frequentist procedure via simulation, it is common to set a parameter to a certain value and evaluate the number of times certain outcomes occur. For example, we can set the difference between two group means to zero, simulate a bunch of p values, and see how many fall below .05. Then we can set the difference to some nonzero number, simulate a bunch of p values, and again see how many are below .05. The first gives you the type-1 error rate for the procedure, and the second gives you the statistical power. This is appropriate for frequentist procedures because the probabilities calculated are always conditional on one or the other hypothesis being true.

One might be tempted to evaluate Bayes factors in the same way; that is, set the difference between two groups to zero and see how many BFs are above some threshold, and then set the difference to something nonzero and see how many BFs are again above some threshold.

The critical error … is studying Bayesian updating conditional on some hypothetical truth rather than conditional on data. This error is easy to make because it is what we have been taught and grown familiar with in our frequentist training. (p. 308)

Evaluating simulations of Bayes factors in this way is incorrect. Bayes factors (and posterior odds) are conditional on only the data observed. In other words, the appropriate evaluation is: “Given that I have observed this data (i.e., BF = x), what is the probability the BF was generated by H1 vs H0?”

Rouder visualizes this as follows. Flip a coin to choose the true hypothesis, then simulate a Bayes factor, and repeat these two steps many many times. At the end of the simulation, whenever BF=x is observed, check and see how many of these came from one model vs the other. The simulation shows that in this scenario if we look at all the times BF=3 is observed, there will be 3 BFs from the true model to every 1 BF from the false model. Since the prior odds are 1 to 1, the posterior odds equals the Bayes factor.

Screenshot 2016-03-06 12.33.59

You can see in the figure above (taken from Rouder’s figure 2), the distribution of Bayes factors observed when the null is true (purple, projected downwards) vs when the alternative is true (pink, projected upwards). Remember, the true hypothesis was chosen by coin flip. You can clearly see that when a BF of 3 to 1 in favor of the null is observed, the purple column is three times bigger than the pink column (shown with the arrows).

Below (taken from Rouder’s figure 2) you see what happens when one employs optional stopping (e.g., flip a coin to pick underlying true model, then sample until BF favors one model to another by at least 10 or you reach a maximum n). The distribution of Bayes factors generated by each model becomes highly skewed, which is often taken as evidence that conclusions drawn from Bayes factors depend on the stopping rule. The incorrect interpretation would be: Given the null is true, the number of times I find BF=x in favor of the alternative (i.e., in favor of the wrong model) has gone up, therefore the BF is sensitive to optional stopping. This is incorrect because it conditions on one model being true and checks the number of times a BF is observed, rather than conditioning on the observed BF and checking how often it came from H0 vs. H1.

Look again at what matters: What is the ratio of observed BFs that come from H1 vs. H0 for a given BF? No matter what stopping rule is used, the answer is always the same: If the true hypothesis is chosen by a coin flip, and a BF of 10 in favor of the alternative is observed, there will be 10 times as many observed BFs in the alternative column (pink) than in the null column (purple).

Screenshot 2016-03-06 12.40.31

In Rouder’s simulations he always used prior odds of 1 to 1, because then the posterior odds equal the Bayes factor. If one were to change the prior odds then the Bayes factor would no longer equal the posterior odds, and the shape of the distribution would again change; but importantly, while the absolute number of Bayes factors that end up in each bin would change, but the ratios of each pink column to purple column would not. No matter what stopping rule you use, the conclusions we draw from Bayes factors and posterior odds are unaffected by the stopping rule.

Feel free to employ any stopping rule you wish.

This result was recently shown again by Deng, Lu, and Chen in a paper posted to arXiv (pdf link) using similar simulations, and they go further in that they prove the theorem.

A few choice quotes

Page 308:

Optional-stopping protocols may be hybrids where sampling occurs until the Bayes factor reaches a certain level or a certain number of samples is reached. Such an approach strikes me as justifiable and reasonable, perhaps with the caveat that such protocols be made explicit before data collection. The benefit of this approach is that more resources may be devoted to more ambiguous experiments than to clear ones.

Page 308:

The critical error … is studying Bayesian updating conditional on some hypothetical truth rather than conditional on data. This error is easy to make because it iswhat we have been taught and grown familiar with in our frequentist training. In my opinion, the key to understanding Bayesian analysis is to focus on the degree of belief for considered models, which need not and should not be calibrated relative to some hypothetical truth.

Page 306-307:

When we update relative beliefs about two models, we make an implicit assumption that they are worthy of our consideration. Under this assumption, the beliefs may be updated regardless of the stopping rule. In this case, the models are dramatically wrong, so much so that the posterior odds contain no useful information whatsoever. Perhaps the more important insight is not that optional stopping is undesirable, but that the meaningfulness of posterior odds is a function of the usefulness of the models being compared.