Significance

A quick comment on recent BF (vs p-value) error control blog posts

Alex Etz Statistics , , , , , ,

There have recently been two stimulating posts regarding error control for Bayes factors. (Stimulating enough to get me to write this, at least.) Daniel Lakens commented on how Bayes factors can vary across studies due to sampling error. Tim van der Zee compared the type 1 and type 2 error rates for using p-values versus using BFs. My comment is not so much to pass judgment on the content of the posts (other than this quick note that they are not really proper Bayesian simulations), but to suggest an easier way to do what they are already doing. They both use simulations to get their error rates (which can take ages when you have lots of groups), but in this post I’d like to show a way to find the exact same answers without simulation, by just thinking about the problem from a slightly different angle.

Lakens and van der Zee both set up their simulations as follows: For a two sample t-test, assume a true underlying population effect size (i.e., δ), a fixed sample size per group (n1 and n2),  and calculate a Bayes factor comparing a point null versus an alternative hypothesis that assigns δ a prior distribution of Cauchy(0, .707) [the default prior for the Bayesian t-test]. Then simulate a bunch of sample t-values from the underlying effect size, plug them into the BayesFactor R package, and see what proportion of BFs are above, below or between certain values (both happen to focus on 3 and 1/3). [This is a very common simulation setup that I see in many blogs these days.]

I’ll just use a couple of representative examples from van der Zee’s post to show how to do this. Let’s say n1 = n2 = 50 and we use the default Cauchy prior on the alternative. In this setup, one can very easily calculate the resulting BF for any observed t-value using the BayesFactor R package. A BF of 3 corresponds to an observed | t | = ~2.47; a BF of 1/3 corresponds to | t | = ~1. These are your critical t values. Any t value greater than 2.47 (or less than -2.47) will have a BF > 3. Any t value between -1 and 1 will have BF < 1/3. Any t value between 1 and 2.47 (or between -1 and -2.47) will have 1/3 < BF < 3. All we have to do now is find out what proportion of sample t values would fall in these regions for the chosen underlying effect size, which is done by finding the area of the sampling distribution between the various critical values.

easier type 1 errors

If the underlying effect size for the simulation is δ = 0 (i.e., the null hypothesis is true), then observed t-values will follow the typical central t-distribution. For 98 degrees of freedom, this looks like the following.

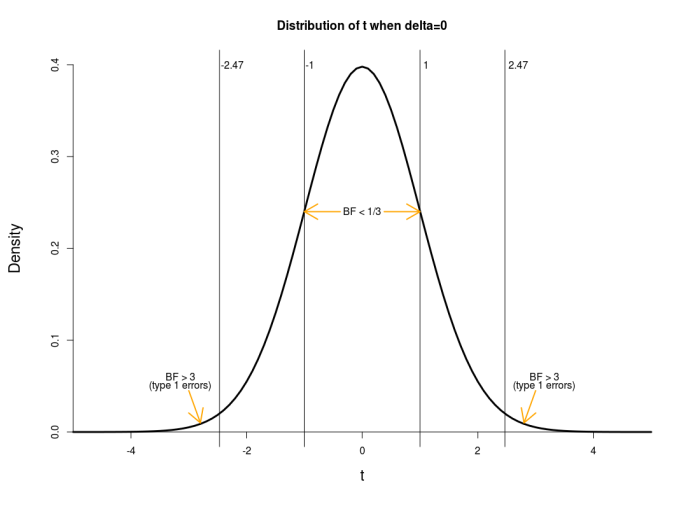
Rplot05

I have marked the critical t values for BF = 3 and BF = 1/3 found above. van der Zee denotes BF > 3 as type 1 errors when δ = 0. The type 1 error rate is found by calculating the area under this curve in the tails beyond | t | = 2.47. A simple line in r gives the answer:

2*pt(-2.47,df=98)
[.0152]

The type 1 error rate is thus 1.52% (van der Zee’s simulations found 1.49%, see his third table). van der Zee notes that this is much lower than the type 1 error rate of 5% for the frequentist t test (the area in the tails beyond | t | = 1.98) because the t criterion is much higher for a Bayes factor of 3 than a p value of .05.  [As an aside, if one wanted the BF criterion corresponding to a type 1 error rate of 5%, it is BF > 1.18 in this case (i.e., this is the BF obtained from | t | = 1.98). That is, for this setup, 5% type 1 error rate is achieved nearly automatically.]

The rate at which t values fall between -2.47 and -1 and between 1 and 2.47 (i.e., find 1/3 < BF < 3) is the area of this curve between -2.47 and -1 plus the area between 1 and 2.47, found by:

2*(pt(-1,df=98)-pt(-2.47,df=98))
[1] 0.3045337

The rate at which t values fall between -1 and 1 (i.e., find BF < 1/3) is the area between -1 and 1, found by:

pt(1,df=98)-pt(-1,df=98)
[1] 0.6802267

easier type 2 errors

If the underlying effect size for the simulation is changed to δ  = .4 (another one of van der Zee’s examples, and now similar to Lakens’s example), the null hypothesis is then false and the relevant t distribution is no longer centered on zero (and is asymmetric). To find the new sampling distribution, called the noncentral t-distribution, we need to find the noncentrality parameter for the t-distribution that corresponds to δ = .4 when n1 = n2 = 50. For a two-sample t test, this is found by a simple formula, ncp = δ / √(1/n1 + 1/n2); in this case we have ncp = .4 / √(1/50 + 1/50) = 2. The noncentral t-distribution for δ=.4 and 98 degrees of freedom looks like the following.

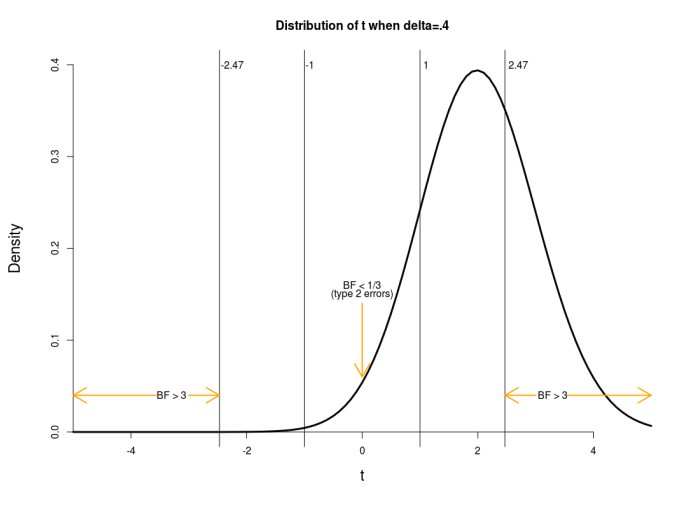
deltazero

I have again marked the relevant critical values. van der Zee denotes BF < 1/3 as type 2 errors when δ ≠ 0 (and Lakens is also interested in this area). The rate at which this occurs is once again the area under the curve between -1 and 1, found by:

pt(1,df=98,ncp=2)-pt(-1,df=98,ncp=2)
[1] 0.1572583

The type 2 error rate is thus 15.7% (van der Zee’s simulation finds 16.8%, see his first table). The other rates of interest are similarly found.

Conclusion

You don’t necessarily need to simulate this stuff! You can save a lot of simulation time by working it out with a little arithmetic plus a few easy lines of code.

 

 

Sunday Bayes: Testing precise hypotheses

Alex Etz Article Review, Statistics , , , , , , ,

First and foremost, when testing precise hypotheses, formal use of P-values should be abandoned. Almost anything will give a better indication of the evidence provided by the data against Ho.

–Berger & Delampady, 1987 (pdf link)

Sunday Bayes series intro:

After the great response to the eight easy steps paper we posted, I started a recurring series, where each week I highlight one of the papers that we included in the appendix of the paper. The format is short and simple: I will give a quick summary of the paper while sharing a few excerpts that I like. If you’ve read our eight easy steps paper and you’d like to follow along on this extension, I think a pace of one paper per week is a perfect way to ease yourself into the Bayesian sphere. At the end of the post I will list a few suggestions for the next entry, so vote in the comments or on twitter (@alxetz) for which one you’d like next. This paper was voted to be the next in the series.

(I changed the series name to Sunday Bayes, since I’ll be posting these on every Sunday.)

Testing precise hypotheses

This would indicate that say, claiming that a P-value of .05 is significant evidence against a precise hypothesis is sheer folly; the actual Bayes factor may well be near 1, and the posterior probability of Ho near 1/2 (p. 326)

Berger and Delampady (pdf link) review the background and standard practice for testing point null hypotheses (i.e., “precise hypotheses”). The paper came out nearly 30 years ago, so some parts of the discussion may not be as relevant these days, but it’s still a good paper.

They start by reviewing the basic measures of evidence — p-values, Bayes factors, posterior probabilities — before turning to an example. Rereading it, I remember why we gave this paper one of the highest difficulty ratings in the eight steps paper. There is a lot of technical discussion in this paper, but luckily I think most of the technical bits can be skipped in lieu of reading their commentary.

One of the main points of this paper is to investigate precisely when it is appropriate to approximate a small interval null hypothesis by using a point null hypothesis. They conclude, that most of the time, the error of approximation for Bayes factors will be small (<10%),

these numbers suggest that the point null approximation to Ho will be reasonable so long as [the width of the null interval] is one-half a [standard error] in width or smaller. (p. 322)

A secondary point of this paper is to refute the claim that classical answers will typically agree with some “objective” Bayesian analyses. Their conclusion is that such a claim

is simply not the case in the testing of precise hypotheses. This is indicated in Table 1 where, for instance, P(Ho | x) [NB: the posterior probability of the null] is from 5 to 50 times larger than the P-value. (p. 318)

They also review some lower bounds on the amount of Bayesian evidence that corresponds to significant p-values. They sum up their results thusly,

The message is simple: common interpretation of P-values, in terms of evidence against precise [null] hypotheses, are faulty (p. 323)

and

the weighted likelihood of H1 is at most [2.5] times that of Ho. A likelihood ratio [NB: Bayes factor] of [2.5] is not particularly strong evidence, particularly when it is [an upper] bound. However, it is customary in practice to view [p] = .05 as strong evidence against Ho. A P-value of [p] = .01, often considered very strong evidence against Ho, corresponds to [BF] = .1227, indicating that H1 is at most 8 times as likely as Ho. The message is simple: common interpretation of P-values, in terms of evidence against precise [null] hypotheses, are faulty (p. 323)

A few choice quotes

Page 319:

[A common opinion is that if] θ0 [NB: a point null] is not in [a confidence interval] it can be rejected, and looking at the set will provide a good indication as to the actual magnitude of the difference between θ and θ0. This opinion is wrong, because it ignores the supposed special nature of θo. A point can be outside a 95% confidence set, yet not be so strongly contraindicated by the data. Only by calculating a Bayes factor … can one judge how well the data supports a distinguished point θ0.

Page 327:

Of course, every statistician must judge for himself or herself how often precise hypotheses actually occur in practice. At the very least, however, we would argue that all types of tests should be able to be properly analyzed by statistics

Page 327 (emphasis original, since that text is a subheading):

[It is commonly argued that] The P-Value Is Just a Data Summary, Which We Can Learn To Properly Calibrate … One can argue that, through experience, one can learn how to interpret P-values. … But if the interpretation depends on Ho, the sample size, the density and the stopping rule, all in crucial ways, it becomes ridiculous to argue that we can intuitively learn to properly calibrate P-values.

page 328:

we would urge reporting both the Bayes factor, B, against [H0] and a confidence or credible region, C. The Bayes factor communicates the evidence in the data against [H0], and C indicates the magnitude of the possible discrepancy.

Page 328:

Without explicit alternatives, however, no Bayes factor or posterior probability could be calculated. Thus, the argument goes, one has no recourse but to use the P-value. A number of Bayesian responses to this argument have been raised … here we concentrate on responding in terms of the discussion in this paper. If, indeed, it is the case that P-values for precise hypotheses essentially always drastically overstate the actual evidence against Ho when the alternatives are known, how can one argue that no problem exists when the alternatives are not known?

Vote for the next entry:

  1. Edwards, Lindman, and Savage (1963) — Bayesian Statistical Inference for Psychological Research (pdf)
  2. Rouder (2014) — Optional Stopping: No Problem for Bayesians (pdf)
  3. Gallistel (2009) — The Importance of Proving the Null (pdf)
  4. Lindley (2000) — The philosophy of statistics (pdf)

The general public has no idea what “statistically significant” means

Alex Etz Article Review, Psychology, Statistics , , ,

The title of this piece shouldn’t shock anyone who has taken an introductory statistics course. Statistics is full of terms that have a specific statistical meaning apart from their everyday meaning. A few examples:

Significant, confidence, power, random, mean, normal, credible, moment, bias, interaction, likelihood, error, loadings, weights, hazard, risk, bootstrap, information, jack-knife, kernel, reliable, validity; and that’s just the tip of the iceberg. (Of course, one’s list gets bigger the more statistics courses one takes.)

It should come as no surprise that the general public mistakes a term’s statistical meaning for its general english meaning when nearly every word has some sort of dual-meaning.

Philip Tromovitch (2015) has recently put out a neat paper in which he surveyed a little over 1,000 members of the general public on their understanding of the meaning of “significant,” a term which has a very precise statistical definition: assuming the null hypothesis is true (usually defined as no effect), discrepancies as large or larger than this result would be so rare that we should act as if the null hypothesis isn’t true and we won’t often be wrong.

However, in everyday english, something that is significant means that it is noteworthy or worth our attention. Rather than give a cliched dictionary definition, I asked my mother what she thought. She says she would interpret a phrase such as, “there was a significant drop in sales from 2013 to 2014” to indicate that the drop in sales was “pretty big, like quite important.” (thanks mom 🙂 ) But that’s only one person. What did Tromovitch’s survey respondents think?

Tromovitch surveyed a total of 1103 people. He asked 611 of his respondents to answer this multiple choice question, and the rest answered a variant as an open ended question. Here is the multiple choice question to his survey respondents:

When scientists declare that the finding in their study is “significant,” which of the following do you suspect is closest to what they are saying:

  • the finding is large
  • the finding is important
  • the finding is different than would be expected by chance
  • the finding was unexpected
  • the finding is highly accurate
  • the finding is based on a large sample of data

Respondents choosing the first two responses were considered to be incorrectly using general english, choosing the third answer was considered correct, and choosing any of the final three were considered other incorrect answer. He separated general public responses from those with doctorate degrees (n=15), but he didn’t get any information on what topic their degree was in, so I’ll just refer to the rest of the sample’s results from here on since the doctorate sample should really be taken with a grain of salt.

Roughly 50% of respondents gave a general english interpretation of the “significant” results (options 1 or 2), roughly 40% chose one of the other three wrong responses (options 4, 5, or 6), and less than 10% actually chose the correct answer (option 3). Even if they were totally guessing you’d expect them to get close to 17% correct (1/6), give or take.

But perhaps multiple choice format isn’t the best way to get at this, since the prompt itself provides many answers that sound perfectly reasonable. Tromovitch also asked this as an open-ended question to see what kind of responses people would generate themselves. One variant of the prompt explicitly mentions that he wants to know about statistical significance, while the other simply mentions significance. The exact wording was this:

Scientists sometimes conclude that the finding in their study is “[statistically] significant.” If you were updating a dictionary of modern American English, how would you define the term “[statistically] significant”?

Did respondents do any better when they can answer freely? Not at all. Neither prompt had a very high success rate; they had correct response rates at roughly 4% and 1%. This translates to literally 12 correct answers out of the total 492 respondents of both prompts combined (including phd responses). Tromovitch includes all of these responses in the appendix so you can read the kinds of answers that were given and considered to be correct.

If you take a look at the responses you’ll see that most of them imply some statement about the probability of one hypothesis or the other being true, which isn’t allowed by the correct definition of statistical significance! For example, one answer coded as correct said, “The likelihood that the result/findings are not due to chance and probably true” is blatantly incorrect. The probability that the results are not due to chance is not what statistical significance tells you at all. Most of the responses coded as “correct” by Tromovitch are quite vague, so it’s not clear that even those correct responders have a good handle on the concept. No wonder the general public looks at statistics as if they’re some hand-wavy magic. They don’t get it at all.

snape 2

My takeaway from this study is the title of this piece: the general public has no idea what statistical significance means. That’s not surprising when you consider that researchers themselves often don’t know what it means! Even professors who teach research methods and statistics get this wrong. Results from Haller & Krauss (2002), building off of Oakes (1986), suggest that it is normal for students, academic researchers, and even methodology instructors to endorse incorrect interpretations of p-values and significance tests. That’s pretty bad. It’s one thing for first-year students or the lay public to be confused, but educated academics and methodology instructors too? If you don’t buy the survey results, open up any journal issue in any psychology journal and you’ll find tons of examples of misinterpretation and confusion.

Recently Hoekstra, Morey, Rouder, & Wagenmakers (2014) demonstrated that confidence intervals are similarly misinterpreted by researchers, despite recent calls (Cumming, 2014) to totally abandon significance tests in lieu of confidence intervals. Perhaps we could toss out the whole lot and start over with something that actually makes sense? Maybe we could try teaching something that people can actually understand?

I’ve heard of this cool thing called Bayesian statistics we could try.

 

References

Cumming, G. (2014). The new statistics: Why and how. Psychological Science, 25(1), 7-29.

Haller, H., & Krauss, S. (2002). Misinterpretations of significance: A problem students share with their teachers. Methods of Psychological Research, 7(1), 1-20.

Hoekstra, R., Morey, R. D., Rouder, J. N., & Wagenmakers, E. J. (2014). Robust misinterpretation of confidence intervals. Psychonomic Bulletin & Review, 21(5), 1157-1164.

Oakes, M. W. (1986). Statistical inference: A commentary for the social and behavioural sciences. Wiley.

Tromovitch, P. (2015). The lay public’s misinterpretation of the meaning of ‘significant’: A call for simple yet significant changes in scientific reporting. Journal of Research Practice, 1(1), 1.

Type-S and Type-M errors

Alex Etz Article Review, Fun Science, Psychology, Statistics , , , , ,
An anonymous reader of the blog emailed me:
 –
I wonder if you’d be ok to help me to understanding this Gelman’s  graph. I struggle to understand what is the plotted distribution and the exact meaning of the red area. Of course I read the related article, but it doesn’t help me much.
Rather than write a long-winded email, I figured it will be easier to explain on the blog using some step by step illustrations. With the anonymous reader’s permission I am sharing the question and this explanation for all to read. The graph in question is reproduced below. I will walk through my explanation by building up to this plot piecewise with the information we have about the specific situation referenced in the related paper. The paper, written by Andrew Gelman and John Carlin, illustrates the concepts of Type-M errors and Type-S errors. From the paper:
–
We frame our calculations not in terms of Type 1 and Type 2 errors but rather Type S (sign) and Type M (magnitude) errors, which relate to the probability that claims with confidence have the wrong sign or are far in magnitude from underlying effect sizes (p. 2)
So Gelman’s graph is an attempt to illustrate these types of errors. I won’t go into the details of the paper since you can read it yourself! I was asked to explain this graph though, which isn’t in the paper, so we’ll go through step by step building our own type-s/m graph in order to build an understanding. The key idea is this: if the underlying true population mean is small and sampling error is large, then experiments that achieve statistical significance must have exaggerated effect sizes and are likely to have the wrong sign. The graph in question:
–
gelmanPlot
–
A few technical details: Here Gelman is plotting a sampling distribution for a hypothetical experiment. If one were to repeatedly take a sample from a population, then each sample mean would be different from the true population mean by some amount due to random variation. When we run an experiment, we essentially pick a sample mean from this distribution at random. Picking at random, sample means tend to be near the true mean of the population, and the how much these random sample means vary follows a curve like this. The height of the curve represents the relative frequency for a sample mean in a series of random picks. Obtaining sample means far away from the true mean is relatively rare since the height of the curve is much lower the farther out we go from the population mean. The red shaded areas indicate values of sample means that achieve statistical significance (i.e., exceed some critical value).
 –
The distribution’s form is determined by two parameters: a location parameter and a scale parameter. The location parameter is simply the mean of the distribution (μ), and the scale parameter is the standard deviation of the distribution (σ). In this graph, Gelman defines the true population mean to be 2 based on his experience in this research area; the standard deviation is equal to the sampling error (standard error) of our procedure, which in this case is approximately 8.1 (estimated from empirical data; for more information see the paper, p. 6). The extent of variation in sample means is determined by the amount of sampling error present in our experiment. If measurements are noisy, or if the sample is small, or both, then sampling error goes up. This is reflected in a wider sampling distribution. If we can refine our measurements, or increase our sample size, then sampling error goes down and we see a narrower sampling distribution (smaller value of σ).

Let’s build our own Type-S and Type-M graph

In Gelman’s graph the mean of the population is 2, and this is indicated by the vertical blue line at the peak of the curve. Again, this hypothetical true value is determined by Gelman’s experience with the topic area. The null hypothesis states that the true mean of the population is zero, and this is indicated by the red vertical line. The hypothetical sample mean from Gelman’s paper is 17, which I’ve added as a small grey diamond near the x-axis. R code to make all figures is provided at the end of this post (except the gif).
–
first_plot
–
If we assume that the true population mean is actually zero (indicated by the red vertical line), instead of 2, then the sampling distribution has a location parameter of 0 and a scale parameter of 8.1. This distribution is shown below. The diamond representing our sample mean corresponds to a fairly low height on the curve, indicating that it is relatively rare to obtain such a result under this sampling distribution.
–
null_plot
–
Next we need to define cutoffs for statistically significant effects (the red shaded areas under the curve in Gelman’s plot) using the null value combined with the sampling error of our procedure. Since this is a two-sided test using an alpha of 5%, we have one cutoff for significance at approximately -15.9 (i.e., 0 – [1.96 x 8.1]) and the other cutoff at approximately 15.9 (i.e., 0 + [1.96 x 8.1]). Under the null sampling distribution, the shaded areas are symmetrical. If we obtain a sample mean that lies beyond these cutoffs we declare our result statistically significant by conventional standards. As you can see, the diamond representing our sample mean of 17 is just beyond this cutoff and thus achieves statistical significance.
–
third_plot
–
But Gelman’s graph assumes the population mean is actually 2, not zero. This is important because we can’t actually have a sign error or a magnitude error if there isn’t a true sign or magnitude. We can adjust the curve so that the peak is above 2 by shifting it over slightly to the right. The shaded areas begin in the same place on the x-axis as before (+/- 15.9), but notice that they have become asymmetrical. This is due to the fact that we shifted the entire distribution slightly to the right, shrinking the left shaded area and expanding the right shaded area.
–
fourth_plot
–
And there we have our own beautiful type-s and type-m graph. Since the true population mean is small and positive, any sample mean falling in the left tail has the wrong sign and vastly overestimates the population mean (-15.9 vs. 2). Any sample mean falling in the right tail has the correct sign, but again vastly overestimates the population mean (15.9 vs. 2). Our sample mean falls squarely in the right shaded tail. Since the standard error of this procedure (8.1) is much larger than the true population mean (2), any statistically significant result must have a sample mean that is much larger in magnitude than the true population mean, and is quite likely to have the wrong sign.
–
In this case the left tail contains 24% of the total shaded area under the curve, so in repeated sampling a full 24% of significant results will be in the wrong tail (and thus be a sign error). If the true population mean were still positive but larger in magnitude then the shaded area in the left tail would become smaller and smaller, as it did when we shifted the true population mean from zero to 2, and thus sign errors would be less of a problem. As Gelman and Carlin summarize,
setting the true effect size to 2% and the standard error of measurement to 8.1%, the power comes out to 0.06, the Type S error probability is 24%, and the expected exaggeration factor is 9.7. Thus, it is quite likely that a study designed in this way would lead to an estimate that is in the wrong direction, and if “significant,” it is likely to be a huge overestimate of the pattern in the population. (p. 6)
I hope I’ve explained this clearly enough for you, anonymous reader (and other readers, of course). Leave a comment below or tweet/email me if anything is unclear!
–
Here is a neat gif showing our progression! Thanks for reading 🙂
–
 plots_gif
 (I don’t think this disclaimer is needed but here it goes: I don’t think people should actually use repeated-sampling statistical inference. This is simply an explanation of the concept. Be a Bayesian!)

R code

#The first plot with the null value and the proposed true value
x <- seq(-35,35,.001) #set up for plotting the curve
y <- dnorm(x,0,8.1) #y values for plotting curve
plot(x=x,y=y, main="Type-S and Type-M error example", xlab="Estimated effect size",
ylab="Relative frequency", type="l", cex.lab=1.5, axes=F, col="white")
axis(1,at=seq(-30,30,10),pos=0) #make the axis nice
axis(2,at=seq(0,.05,.01),pos=-35,las=1) #make the axis nice
lines(c(0,0),c(0,.05),col="red",lwd=3) ##Add line at null value
lines(c(2,2),c(0,.05),col="blue",lwd=3) ##Add line at population mean
points(17, .001, pch=23, bg="grey",col="black",cex=1.5) ##Add sample mean
#######################################################################################################
##The second and third plots with the null sampling distribution and significance areas under the curve
x <- seq(-35,35,.001) #set up for plotting the curve
y <- dnorm(x,0,8.1) #y values for plotting curve
plot(x,y, main="Type-S and Type-M error example", xlab="Estimated effect size",
ylab= "Relative frequency", type="l",cex.lab=1.5, las=1, lwd=3, axes = F)
axis(1,at=seq(-30,30,10),pos=0) #make the x axis nice
axis(2,at=seq(0,.05,.01),pos=-35,las=1) #make the y axis nice
lines(c(0,0),c(0,dnorm(0,0,8.1)),col="red",lwd=3) ##adds null line
lines(c(2,2),c(0,dnorm(2,0,8.1)),col="blue",lwd=3) ##adds true pop mean line
points(17, .001, pch=23, bg="grey",col="black",cex=1.5) ##adds sample mean
##Adds shaded area
cord.x <- c(-35, seq(-35,-15.9,.01),-15.9) ##set up for shading
cord.y <- c(0,dnorm(seq(-35,-15.9,.01),0,8.1),0) ##set up for shading
polygon(cord.x,cord.y,col='red') ##shade left tail
cord.xx <- c(35, seq(35,15.9,-.01),15.9)
cord.yy <- c(0,dnorm(seq(35,15.9,-.01),0,8.1),0)
polygon(cord.xx,cord.yy,col='red') ##shade right tail
points(17, .001, pch=23, bg="grey",col="black",cex=1.5) ##replots the sample mean over the shading
#######################################################################################################
##The fourth plot with the alternative sampling distribution and significance areas under the curve
x <- seq(-35,35,.001) #set up for plotting the curve
y <- dnorm(x,2,8.1) #y values for plotting curve
plot(x,y, main="Type-S and Type-M error example", xlab="Estimated effect size",
ylab= "Relative frequency", type="l", cex.lab=1.5, las=1, lwd=3, axes = F)
axis(1,at=seq(-30,30,10),pos=0) #make the x axis nice
axis(2,at=seq(0,.05,.01),pos=-35, las=1) #make the y axis nice
lines(c(0,0),c(0,dnorm(0,2,8.1)),col="red",lwd=3) ##add vertical line at null value
lines(c(2,2),c(0,dnorm(2,2,8.1)),col="blue",lwd=3) ##add vertical line at population mean
cord.x <- c(-35, seq(-35,-15.9,.01),-15.9) ##set up for shading
cord.y <- c(0,dnorm(seq(-35,-15.9,.01),2,8.1),0) ##set up for shading
polygon(cord.x,cord.y,col='red') ##shade left tail
cord.xx <- c(35, seq(35,15.9,-.01),15.9)
cord.yy <- c(0,dnorm(seq(35,15.9,-.01),2,8.1),0)
polygon(cord.xx,cord.yy,col='red') ##shade right tail
points(17, .001, pch=23, bg="grey",col="black", cex=1.5) ##replots sample mean over shading
view raw gistfile1.txt hosted with ❤ by GitHub

Edwards, Lindman, and Savage (1963) on why the p-value is still so dominant

Alex Etz Psychology, Statistics , , , , , , ,

Below is an excerpt from Edwards, Lindman, and Savage (1963, pp. 236-7), on why p-value procedures continue to be dominant in the empirical sciences even after it has been repeatedly shown to be an incoherent and nonsensical statistic (note: those are my choice of words, the authors are very cordial in their commentary). The age of the article shows in numbers 1 and 2, but I think it is still valuable commentary; Numbers 3 and 4 are still highly relevant today.

From Edwards, Lindman, and Savage (1963, pp. 236-7):

If classical significance tests have rather frequently rejected true null hypotheses without real evidence, why have they survived so long and so dominated certain empirical sciences ? Four remarks seem to shed some light on this important and difficult question.

1. In principle, many of the rejections at the .05 level are based on values of the test statistic far beyond the borderline, and so correspond to almost unequivocal evidence [i.e., passing the interocular trauma test]. In practice, this argument loses much of its force. It has become customary to reject a null hypothesis at the highest significance level among the magic values, .05, .01, and .001, which the test statistic permits, rather than to choose a significance level in advance and reject all hypotheses whose test statistics fall beyond the criterion value specified by the chosen significance level. So a .05 level rejection today usually means that the test statistic was significant at the .05 level but not at the .01 level. Still, a test statistic which falls just short of the .01 level may correspond to much stronger evidence against a null hypothesis than one barely significant at the .05 level. …

2. Important rejections at the .05 or .01 levels based on test statistics which would not have been significant at higher levels are not common. Psychologists tend to run relatively large experiments, and to get very highly significant main effects. The place where .05 level rejections are most common is in testing interactions in analyses of variance—and few experimenters take those tests very seriously, unless several lines of evidence point to the same conclusions. [emphasis added]

3. Attempts to replicate a result are rather rare, so few null hypothesis rejections are subjected to an empirical check. When such a check is performed and fails, explanation of the anomaly almost always centers on experimental design, minor variations in technique, and so forth, rather than on the meaning of the statistical procedures used in the original study.

4. Classical procedures sometimes test null hypotheses that no one would believe for a moment, no matter what the data […] Testing an unbelievable null hypothesis amounts, in practice, to assigning an unreasonably large prior probability to a very small region of possible values of the true parameter. […]The frequent reluctance of empirical scientists to accept null hypotheses which their data do not classically reject suggests their appropriate skepticism about the original plausibility of these null hypotheses. [emphasis added]

 

References

Edwards, W., Lindman, H., & Savage, L. J. (1963). Bayesian statistical inference for psychological research. Psychological review, 70(3), 193-242.